Interpolasi
adalah proses menemukan dan mengevaluasi fungsi yang grafiknya melewati
himpunan titik-titik yang diberikan. Interpolasi digunakan untuk
memperkirakan suatu fungsi hanya dengan data-data yang telah diketahui.
Pada tulisan ini akan dibahas Interpolasi Lagrange atau dikenal juga dengan nama Polinom Lagrange. Perhatikan Polinom Lagrange Derajat 1 atau Interpolasi Linier,
untuk interpolasi ini menggunakan pendekatan garis-gari atau persamaan
linier sehingga digunakan persamaan garis untuk mengkonstruksi
interpolasinya. Misal kita punya dua titik yaitu (x0, y0) dan (x1, y1), sehingga masing-masing titik dapat ditulis sebagai berikut :
P1(x0) = y0 = a0 + a1x0 … (i)
P1(x1) = y1 = a0 + a1x1 … (ii)
Kemudian eliminasi kedua persamaan,
y0 = a0 + a1x0
y1 = a0 + a1x1 -
y0 – y1 = a1x0 – a1x1
a1 = 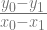
kemudian substitusi ke persamaan (i)
y0 = a0 +  x0
x0
a0 = y0 –  x0
x0
=  y0 –
y0 –  x0
x0
= 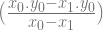 –
– 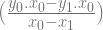
= 
substitusi nilai a0 dan a1 ke persamaan umum polinom p1(x), sehingga :
P1(x) = a0 + a1x
=  +
+  x
x
=  +
+ 
= 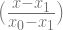 y0 +
y0 +  y1
y1
= 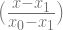 y0 +
y0 +  y1
y1
= 1L0 (x) + 1L1 (x)
Kemudian untuk Interpolasi Lagrange dengan menggunakan Polinom Derajar 2 atau dikenal juga dengan Interpolasi Kuadrat. Fungsi yang akan dikontruksi ini menggunakan tiga titik. Misal titik-titik tersebut adalah (x0, y0), (x1, y1) dan (x2, y2) dengan x0 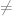 x1
x1 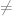 x2.
x2.
P2(x0) = y0 = a0 + a1x0 + a2x02 … (i)
P2(x1) = y1 = a0 + a1x1 + a2x12 … (ii)
P2(x2) = y2 = a0 + a1x2 + a2x22… (iii)
dengan mengeliminasi persamaan (i), (ii) dan (iii), maka akan diperoleh
a0 = 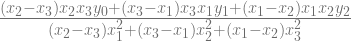
a1 = 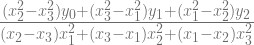
a2 = 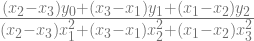
kemudian substitusikan nilai a0, a1 dan a2 ke persamaan P2(x) = a0 + a1x + a2x2, sehingga diperoleh :
P2(x) = ![[\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}] [\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_1%29%28x-x_2%29%7D%7B%28x_0-x_1%29%28x_0-x_2%29%7D%5D+&bg=ffffff&fg=666666&s=2) y0 +
y0 + ![[\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}] [\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_0%29%28x-x_2%29%7D%7B%28x_1-x_0%29%28x_1-x_2%29%7D%5D+&bg=ffffff&fg=666666&s=2) y1 +
y1 + ![[\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}] [\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_0%29%28x-x_1%29%7D%7B%28x_2-x_0%29%28x_2-x_1%29%7D%5D+&bg=ffffff&fg=666666&s=2) y2
y2
= 2L0 (x) + 2L1 (x) + 2L2 (x)
Kemudian untuk polinom derajat 3 atau menggunakan 4 titik yaitu dengan (x0, y0), (x1, y1), (x2, y2), dan (x3, y3) dengan x0 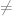 x1
x1 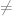 x2
x2 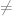 x3, diperoleh rumusnya sebagai berikut.
x3, diperoleh rumusnya sebagai berikut.
P3(x) = ![[\frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}] [\frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_1%29%28x-x_2%29%28x-x_3%29%7D%7B%28x_0-x_1%29%28x_0-x_2%29%28x_0-x_3%29%7D%5D+&bg=ffffff&fg=666666&s=2) y0 +
y0 + ![[\frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}] [\frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_0%29%28x-x_2%29%28x-x_3%29%7D%7B%28x_1-x_0%29%28x_1-x_2%29%28x_1-x_3%29%7D%5D+&bg=ffffff&fg=666666&s=2) y1 +
y1 + ![[\frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}] [\frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_0%29%28x-x_1%29%28x-x_3%29%7D%7B%28x_2-x_0%29%28x_2-x_1%29%28x_2-x_3%29%7D%5D+&bg=ffffff&fg=666666&s=2) y2 +
y2 + ![[\frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}] [\frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_0%29%28x-x_1%29%28x-x_2%29%7D%7B%28x_3-x_0%29%28x_3-x_1%29%28x_3-x_2%29%7D%5D+&bg=ffffff&fg=666666&s=2) y3
y3
= 3L0 (x) + 3L1 (x) + 3L2 (x) + 3L3 (x)
Secara umum maka rumus untuk Interpolasi Lagrange adalah sebagai berikut :
Jika k < n, diperoleh.
nLk (x) = 
Contoh 1 :
Konstruksikan P2(x) dari titik yang diketahui berikut (0, -1),(1, -1) dan (2, 7) !
Penyelesaian :
Karena diketahui 3 titik yaitu (x0, y0) = (0, -1), (x1, y1) = (1, -1) dan (x2, y2) = (2, 7) maka digunakan rumus
P2(x) = 2L0 (x) + 2L1 (x) + 2L2 (x)
dengan,
2L0 (x) = ![[\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}] [\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_1%29%28x-x_2%29%7D%7B%28x_0-x_1%29%28x_0-x_2%29%7D%5D+&bg=ffffff&fg=666666&s=2) y0
y0
= ![[\frac{(x-1)(x-2)}{(0-1)(0-2)}] [\frac{(x-1)(x-2)}{(0-1)(0-2)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-1%29%28x-2%29%7D%7B%280-1%29%280-2%29%7D%5D+&bg=ffffff&fg=666666&s=2) (-1)
(-1)
= ![[\frac{x^2-3x+2}{2}] [\frac{x^2-3x+2}{2}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7Bx%5E2-3x%2B2%7D%7B2%7D%5D+&bg=ffffff&fg=666666&s=2) (-1)
(-1)
= 
2L1 (x) = ![[\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}] [\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_0%29%28x-x_2%29%7D%7B%28x_1-x_0%29%28x_1-x_2%29%7D%5D+&bg=ffffff&fg=666666&s=2) y1
y1
= ![[\frac{(x-0)(x-2)}{(1-0)(1-2)}] [\frac{(x-0)(x-2)}{(1-0)(1-2)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-0%29%28x-2%29%7D%7B%281-0%29%281-2%29%7D%5D+&bg=ffffff&fg=666666&s=2) (-1)
(-1)
= ![[\frac{x^2-2x}{-1}] [\frac{x^2-2x}{-1}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7Bx%5E2-2x%7D%7B-1%7D%5D+&bg=ffffff&fg=666666&s=2) (-1)
(-1)
= 
2L2 (x) = ![[\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}] [\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_0%29%28x-x_1%29%7D%7B%28x_2-x_0%29%28x_2-x_1%29%7D%5D+&bg=ffffff&fg=666666&s=2) y2
y2
= ![[\frac{(x-0)(x-1)}{(2-0)(2-1)}] [\frac{(x-0)(x-1)}{(2-0)(2-1)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-0%29%28x-1%29%7D%7B%282-0%29%282-1%29%7D%5D+&bg=ffffff&fg=666666&s=2) (7)
(7)
= ![[\frac{x^2-x}{2}] [\frac{x^2-x}{2}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7Bx%5E2-x%7D%7B2%7D%5D+&bg=ffffff&fg=666666&s=2) (7)
(7)
= 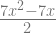
P2(x) =  +
+  +
+ 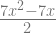
= 
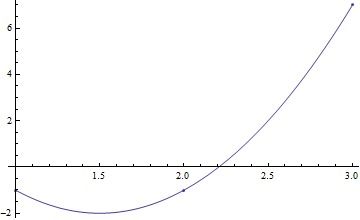
= 4x2 – 4x – 1
grafik hasil interpolasi
Contoh 2 :
Tentukan polinom yang menginterpolasi fungsi f(x) = cos x pada titik-titik x = {0, 1/3, 2/3, 1}
Penyelesaian :
Karena yang diketahui nilai “x”-nya saja, berarti dihitung dulu nilai y atau f(x).
y0 = cos (0) = 1
y1 = cos (1/3) = 0.95
y2 = cos (2/3) = 0.79
y3 = cos (1) = 0.54
P3(x) = 3L0 (x) + 3L1 (x) + 3L2 (x) + 3L2 (x), dengan
3L0 (x) = ![[\frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}] [\frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_1%29%28x-x_2%29%28x-x_3%29%7D%7B%28x_0-x_1%29%28x_0-x_2%29%28x_0-x_3%29%7D%5D+&bg=ffffff&fg=666666&s=2) y0
y0
= ![[\frac{(x-\frac{1}{3})(x-\frac{2}{3})(x-1)}{(0-\frac{1}{3})(0- \frac{2}{3})(0-1)}] [\frac{(x-\frac{1}{3})(x-\frac{2}{3})(x-1)}{(0-\frac{1}{3})(0- \frac{2}{3})(0-1)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-%5Cfrac%7B1%7D%7B3%7D%29%28x-%5Cfrac%7B2%7D%7B3%7D%29%28x-1%29%7D%7B%280-%5Cfrac%7B1%7D%7B3%7D%29%280-+%5Cfrac%7B2%7D%7B3%7D%29%280-1%29%7D%5D+&bg=ffffff&fg=666666&s=2) (1)
(1)
= 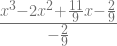
= 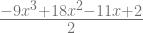
3L1 (x) = ![[\frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}] [\frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_0%29%28x-x_2%29%28x-x_3%29%7D%7B%28x_1-x_0%29%28x_1-x_2%29%28x_1-x_3%29%7D%5D+&bg=ffffff&fg=666666&s=2) y1
y1
= ![[\frac{(x-0)(x-\frac{2}{3})(x-1)}{(\frac{1}{3}-0)(\frac{1}{3}-\frac{2}{3})(\frac{1}{3}-1)}] [\frac{(x-0)(x-\frac{2}{3})(x-1)}{(\frac{1}{3}-0)(\frac{1}{3}-\frac{2}{3})(\frac{1}{3}-1)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-0%29%28x-%5Cfrac%7B2%7D%7B3%7D%29%28x-1%29%7D%7B%28%5Cfrac%7B1%7D%7B3%7D-0%29%28%5Cfrac%7B1%7D%7B3%7D-%5Cfrac%7B2%7D%7B3%7D%29%28%5Cfrac%7B1%7D%7B3%7D-1%29%7D%5D+&bg=ffffff&fg=666666&s=2) (0.95)
(0.95)
= ![[\frac{x^3-\frac{5}{3}x^2+\frac{2}{3}x}{\frac{2}{27}}] [\frac{x^3-\frac{5}{3}x^2+\frac{2}{3}x}{\frac{2}{27}}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7Bx%5E3-%5Cfrac%7B5%7D%7B3%7Dx%5E2%2B%5Cfrac%7B2%7D%7B3%7Dx%7D%7B%5Cfrac%7B2%7D%7B27%7D%7D%5D+&bg=ffffff&fg=666666&s=2) (0.95)
(0.95)
= ![[\frac{27x^3-45x^2+18x}{2}] [\frac{27x^3-45x^2+18x}{2}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B27x%5E3-45x%5E2%2B18x%7D%7B2%7D%5D+&bg=ffffff&fg=666666&s=2) (0.95)
(0.95)
= 
3L2 (x) = ![[\frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}] [\frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_0%29%28x-x_1%29%28x-x_3%29%7D%7B%28x_2-x_0%29%28x_2-x_1%29%28x_2-x_3%29%7D%5D+&bg=ffffff&fg=666666&s=2) y2
y2
= ![[\frac{(x-0)(x-\frac{1}{3})(x-1)}{(\frac{2}{3}-0)(\frac{2}{3}-\frac{1}{3})(\frac{2}{3}-1)}] [\frac{(x-0)(x-\frac{1}{3})(x-1)}{(\frac{2}{3}-0)(\frac{2}{3}-\frac{1}{3})(\frac{2}{3}-1)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-0%29%28x-%5Cfrac%7B1%7D%7B3%7D%29%28x-1%29%7D%7B%28%5Cfrac%7B2%7D%7B3%7D-0%29%28%5Cfrac%7B2%7D%7B3%7D-%5Cfrac%7B1%7D%7B3%7D%29%28%5Cfrac%7B2%7D%7B3%7D-1%29%7D%5D+&bg=ffffff&fg=666666&s=2) (0.79)
(0.79)
= ![[\frac{x^3-\frac{4}{3}x^2+\frac{1}{3}x}{-\frac{2}{27}}] [\frac{x^3-\frac{4}{3}x^2+\frac{1}{3}x}{-\frac{2}{27}}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7Bx%5E3-%5Cfrac%7B4%7D%7B3%7Dx%5E2%2B%5Cfrac%7B1%7D%7B3%7Dx%7D%7B-%5Cfrac%7B2%7D%7B27%7D%7D%5D+&bg=ffffff&fg=666666&s=2) (0.79)
(0.79)
= ![[\frac{-27x^3+36x^2-9x}{2}] [\frac{-27x^3+36x^2-9x}{2}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B-27x%5E3%2B36x%5E2-9x%7D%7B2%7D%5D+&bg=ffffff&fg=666666&s=2) (0.79)
(0.79)
= 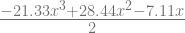
3L3 (x) = ![[\frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x-x_2)}] [\frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x-x_2)}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-x_0%29%28x-x_1%29%28x-x_2%29%7D%7B%28x_3-x_0%29%28x_3-x_1%29%28x-x_2%29%7D%5D+&bg=ffffff&fg=666666&s=2) y3
y3
= ![[\frac{(x-0)(x-\frac{1}{3})(x-\frac{2}{3})}{(1-0)(1-\frac{1}{3})(1-\frac{2}{3})}] [\frac{(x-0)(x-\frac{1}{3})(x-\frac{2}{3})}{(1-0)(1-\frac{1}{3})(1-\frac{2}{3})}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%28x-0%29%28x-%5Cfrac%7B1%7D%7B3%7D%29%28x-%5Cfrac%7B2%7D%7B3%7D%29%7D%7B%281-0%29%281-%5Cfrac%7B1%7D%7B3%7D%29%281-%5Cfrac%7B2%7D%7B3%7D%29%7D%5D+&bg=ffffff&fg=666666&s=2) (0.54)
(0.54)
= ![[\frac{x^3-x^2+\frac{2}{9}x}{\frac{2}{9}}] [\frac{x^3-x^2+\frac{2}{9}x}{\frac{2}{9}}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7Bx%5E3-x%5E2%2B%5Cfrac%7B2%7D%7B9%7Dx%7D%7B%5Cfrac%7B2%7D%7B9%7D%7D%5D+&bg=ffffff&fg=666666&s=2) (0.54)
(0.54)
= ![[\frac{9x^3-9x^2+2x}{2}] [\frac{9x^3-9x^2+2x}{2}]](http://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B9x%5E3-9x%5E2%2B2x%7D%7B2%7D%5D+&bg=ffffff&fg=666666&s=2) (0.54)
(0.54)
= 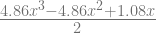
P3(x) = 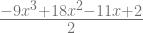 +
+  +
+ 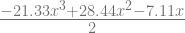 +
+ 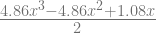
= 
= 0.09x3 – 0.585x2 + 0.035x + 1
Tidak ada komentar:
Posting Komentar